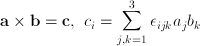Símbolo de Levi-Civita — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar … Wikipedia Español
Tullio Levi-Civita — Nacimiento 29 de Marzo, 1873 Padua Fallecimiento 29 de Diciembre, 1941 Roma Nacionalidad Italiano Campo matemáticas … Wikipedia Español
Delta de Kronecker — Saltar a navegación, búsqueda En matemática, la delta de Kronecker es una función de dos variables, que vale 1 si son iguales, y 0 si son diferentes. Se escribe con el símbolo y se usa como una taquigrafía notacional más que como función. Se la… … Wikipedia Español
Momento angular — El momento angular o momento cinético es una magnitud física importante en todas las teorías físicas de la mecánica, desde la mecánica clásica a la mecánica cuántica, pasando por la mecánica relativista. Su importancia en todas ellas se debe a… … Wikipedia Español
Álgebra multilineal — En la matemática, el álgebra multilineal es una área de estudio que generaliza los métodos del álgebra lineal. Los objetos de estudio son los productos tensoriales de espacios vectoriales y las transformaciones multi lineales entre los espacios.… … Wikipedia Español
Ecuación de Rarita-Schwinger — Saltar a navegación, búsqueda En física teórica, la ecuación de Rarita Schwinger es la ecuación de evolución temporal relativista que describe partículas fermiónicas de espín 3/2, formulada en 1941 por William Rarita and Julian Schwinger. Es… … Wikipedia Español
Gradiente — En cálculo vectorial, el gradiente de un campo escalar f es un campo vectorial. El vector gradiente de f evaluado en un punto genérico x del dominio de f, (x), indica la dirección en la cual el campo f varía más rápidamente y su módulo representa … Wikipedia Español
Hamiltoniano molecular — Este artículo o sección necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 14 de septiembre de 2011. También puedes ayudar… … Wikipedia Español
Matrices de Pauli — Las matrices de Pauli, deben su nombre a Wolfgang Ernst Pauli, son matrices usadas en física cuántica en el contexto del momento angular intrínseco o espín. Matemáticamente, las matrices de Pauli constituyen una base vectorial del álgebra de Lie… … Wikipedia Español
Rotacional — Saltar a navegación, búsqueda En el cálculo vectorial, el rotacional o rotor es un operador vectorial que muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto. Contenido 1 Introducción 1.1 Fuente vectorial y escalar … Wikipedia Español
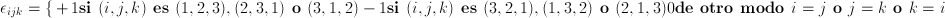 nombrado así por Tullio Levi-Civita. Se utiliza en muchas áreas de las matemáticas y en física. Por ejemplo, en álgebra lineal, el producto cruzado de dos vectores se puede escribir como:
nombrado así por Tullio Levi-Civita. Se utiliza en muchas áreas de las matemáticas y en física. Por ejemplo, en álgebra lineal, el producto cruzado de dos vectores se puede escribir como:
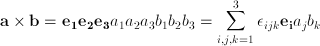 o más simplemente:
o más simplemente: